Cuando les matemátiques faen arte: sobre la complexidá y guapura de los fractales
Fai munchos años que Mandelbrot asoleyó’l so primer trabayu sobre fractales, yera l'añu 1975, y d’aquella nun fue quien a dar una definición formal de lo que ye un fractal. Nun tardó muncho en vese obligáu a dala d’una manera formal, que separtase los oxetos fractales de los que nun lo son. Parte de la definición falaba de coses que ya vimos (la dimensión, l’autosimilitú,...). A la vez, entamó un procesu d’estudiu sofitáu nes imáxenes xeneraes con una teunoloxía qu'entá taba en faches, pero que foi una ferramienta perimportante: los ordenadores. Lo qu’alcontró foi un mundiu onde se trafulquen matemátiques y arte.
Tenemos pernidiu ya’l métodu pa facer un fractal repetir y repetir una aición; fasta agora ficímoslo con imáxenes, pero ¿qué pasa si lo facemos con númberos?La idea ye percenciella, garramos un númberu y aplicamos una operación, siempre la mesma, un númberu determináu de vegaes.
Vamos representar esto de manera formal escribiendo:
Podemos pensar na operación de suma-y dos a x:
Si entamamos en 1, aplicamosla cinco veces tenemos:
x0=1, x1=3, x2=5, x3=7, x4=9, x5=11
Xeneramos dellos númberos que denomamos órbita de la iteración, el puntu pa onde va ésta ye l´’atrautor, que nesti casu si iteramos infinites veces ye infinitu.
Esto nun ye asina siempre, si per exemplu tenemos
y entamanos con 0,5 la órbita de la iteración ye 0,5; 0,25; 0,0625; 0,003906... Polo que l’atrautor ye 0. Pero si en vez de 0,5 aniciamos con 1, caúna de les iteraciones que fagamos va tener como resultáu 1, esto ye lo que nomen puntu fixu.
Hai milenta operaciones que podemos facer col fin d’estudiar les órbites, puntos fixos y atrautores de distintes tribes de númberos, quiciabes los que meyores resultaos dan ye’l grupu de la númberos complexos, colos que Mandelbrot esploró un colmiellu de posibilidaes. Vamos facer una parada col fin de quita-y el polvu al conceutu de númberu complexu.
Una manera de determinar una posición nuna reuta ye dividila en partes iguales y etiquetar caúna d’estes partes, esto define’l sistema numbéricu que nós usamos, la primer parte ye’l 1, per exemplu, llueu vien el 2, etc. Podemos trabayar con estes entidaes, nomaes númberos, faciendo-yos delles operaciones.
Asemeyáu ye’l conceutu de númberu complexu, anque en vez de trabayar sobre una llinia trabayamos sobre un planu, que nomamos complexu. Cuando tratamos de dicir en qué llugar tamos podemos dar unes coordenaes, una pal llargor y otra pal anchor, polo que tenemos un númberu (de la forma (x,y)) que danos la posición. Nel planu complexu facemos lo mesmo, un númberu da la parte real (posición na reuta real que vimos antes) y otru da la imaxinaria (sacáu d’una reuta perpendicular a la real). Les regles pa operar con estos númberos son distintes que les qu’usamos colos que formen la reuta real, y dan siempre otros númberos complexos.
Vamos recuperar la fórmula del aniciu
y aplicámos-y el siguiente operador
L’elementu z ye un complexu, y c ye una constante, que ye tamién un númberu complexu. La fórmula diz: eleva al cuadráu un númberu complexu y suma-y la constante c.
Pa un aniciu con z=(1,0) y c=(0,1) tenemos una órbita de (1,1), (0,3), (-9,1), (80,-17)... Si iteramos el suficiente númberu de veces vemos que cada vegada tamos más lloñe del orixen (0,0) anque ensin dir p’hacia nengún númberu concretu, tamién vamos ver que l’atrautor ye’l infinitu. Por mor al so comportamientu podemos nomar a esta triba númberos "fugaos".
En xeneral, los puntos del planu complexu xeneren órbites que tienen esti comportamientu, con una salvedá. Hai dellos puntos nos qu’apaecen puntos fixos, órbites periódiques y atrautores finitos. Podemos nomalos númberos "presos", ya que nun son quien a salir d’esa rexón.
La comuña formada polos númberos presos fai una llende zarrada nel espaciu complexu que separta a éstos de los fugaos. Son los denomaos conxuntos de Julia, en honor al so descubridor.
 |
| Dellos conxuntos de Julia |
Tou esto ye perguapu, pero ¿qué tien que ver colos fractales? Si miramos la llende ente los fugaos y los presos, y nos vamos averando vamos atopar qu’esa llinia ye un fractal, y cualesquier cachu d’ella va rexenerar el tou. El fractal qu’apaez tien dellos niveles d´’autosimilitú, ye dicir pasa por delles estructures antes de volver a repetise igual.
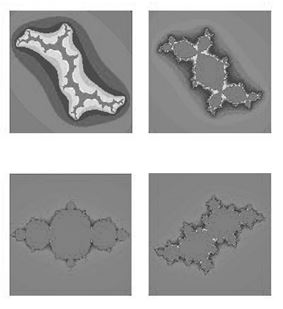 |
| Conxuntos de Julia |
Hai que rescamplar la intuición de Gaston Julia, cuando estudió’l comportamientu d’estes funciones (tamos falando de les primeres décades de sieglu XX) nun había ordenadores que dibuxasen la llende del conxuntu. Les representaciones gráfiques nun apaecieron fasta los setenta y ochenta del sieglu XX, cuando Mandelbrot y Hubbart, enseñaron al mundiu les semeyes d’estos nuevos mostruos.
Los exemplos de conxuntos de Julia que vimos fasta agora nun son más qu’una amuesa de los posibles conxuntos que puen xenerase, esiste un mundiu de posibilidaes que xeneren un númberu encomanáu de conxuntos, fechu que convida a clasificalos.
Si echamos una güeyada a los dibuxos d’arriba, podemos cayer na cuenta que pue facese una primer clasificación: per un llau los conxuntos que llenden una superficie única (conexos), y per otru los que divídense en cachos, y que van dir rompiéndose en cachos infinitos (disconexos).
D’ésto diose cuenta Mandelbrot, y sofitáu coles matemátiques qu’hubiera desendolcáu Julia (y per separáu, anque a la vez, Fatou), buscó valores de la constante c que daben como resultáu un conxuntu conexu.
El resultáu’l siguiente conxuntu, que se-y nomó desde aquella Conxuntu de Mandelbrot:
 |
| Conxuntu de Mandelbrot |
Esti conxuntu ta formáu infinitos númberos complexos, polo que la imaxen permite una grau d’ampliación tamién infinitu. Ya nun nos tien qu’asustar dicir que tamos delantre d’una figura con una llende infinita. En cuanto a la so fractalidá, anque ye una fractal ye d’una triba particular la fractales no lliniales. Nellos l’autosimilitú desapaez, con cada averamientu vemos que se produz un cambiu nos rasgos de la llende. Esto nun sigue patrones aleatorios, sinón que van dir apaeciendo (codificaes) les propiedaes de caún de los conxuntos de Julia.
 |
| Conxuntu de Mandelbrot y dellos conxuntos de Julia que resulten de “traducir” dellos cachos de la llende |
Depués definir esti conxuntu, Mandelbrot y otros atoparon otros conxuntos de la mesma triba, coles mesmes propiedaes que la orixinal.
 |
| Conxuntu de Mandelbrot y los sos hermanos |
L’oxetu d’esti ensayu nun ye mostrar tola dimensión de los fractales equí espuestos, por eso pal que tea interés por ver distintes ampliaciones de los conxuntos de Julia y Mandelbrot encamentámoslu que busque n’internet, onde de xuru va atopar milenta imáxenes que van satisfacelu enforma, y sobre tou videos (p. ex. en Youtube) onde va poder ver animaciones d’ampliación d’estos y otros fractales.
Pue ser qu’el llector tea un poco fartu d’oxetos matemáticos abstrautos que nun tienen que ver col mundiu físicu, ye hora d’abaxanos de la ñube, y posar los pies en suelu, y aplicar tolos que vimos al estudiu de na natura, agora entama lo guapu de verdá...





Comentarios
Publicar un comentario