Ecosistemes, desaniciu y economía: dinámica fractal de sistemes complexos
Hasta agora tuvimos falando del estudiu y la interpretación d’oxetos y estructures desde puntu de vista fractal pol mediu de métodos gráficos como’l Cuenta-caxes o los Multifractales aplicables a semeyes o representaciones. Pero, hai coses a les que nun se-yos pue facer una semeya, como per exemplu los procesos dinámicos. Desde bien ceo matemáticos y otros estudiosos ya aguriaben que los procesos naturales seguíen unes pautes, anque abegoses d’atalantar. Tales como les relaciones que caltienen los seres vivos nos ecosistemes. Vamos averanos a esti problema.
Podemos garrar como elementu mínimu del ecosistema a una población d’una especie cualesquiera. L’estáu de la población bien dao pol númberu de ñacimientos y el de muertes (seyan pola causa que seyan), siendo Ni la población nel añu i. Podemos esperar qu’el númberu d’animales na siguiente xeneración sedrá proporcional a la del añu anterior, podemos escribir:
onde a ye una constante que describe esa proporcionalidá qu’espresa la capacidá reproductiva de la especie.
Si aplicamos esta fórmula vamos ver que la población subi ensin parar, falta algo pa que seya una descripción asemeyada a la natura. Falten los muertos por fame, por depredación y por vieyera. Ye nidiu que cuánto mayor ye la población más brenga hai ente los indivíduos pola comida, por llugares onde vivir o criar, polo cuál, nun ye descabelláu que la probabilidá de que muerra un individuu tea venceyada al númberu d’indivíduos de la población d’esi añu y del anterior, podemos escribir entós:
au b ye una constante que describi esa proporcionalidá, qu’espresa la tasa de muertes.
Si agora axuntamos les dos espresiones tenemos:
Esta fórmula describi un modelu de simulación, cenciellu, de la dinámica de población. Si iteramos el modelu podemos conocer la evolución de la población a lo llargo’l tiempu.
Pa nun enguedeyar muncho les coses, vamos estudiar un modelu cenciellu, onde les constantes a y b son iguales, y el valor de la población ta normalizáu (o sía que ta ente 0 y 1), con ello vamos poder llegar al inquiz de la entruga ensin munches torgues. Con estes normes la ecuación quedanos en:
Los resultaos de caúna de les iteraciones van dar un valor ente 0 y 1, siendo 0 el desaniciu d’esa población y 1 el valor máximu d’ella.
Pa muestra un botón. Con a=2,5 y Ni=0,7 tenemos los siguientes resultaos:
El resultáu ye nidio, la población va estabilizándose fasta un valor que nun camuda (si nos alcordamos nómase puntu fixu, y ye un atrautor). Esto tamién socede si caltenemos el valor de a y camudamos N, el resultáu caberu siempre ye 0,6, anque la población seya lo grande que queramos.
¿Qué socede si cambiamos el valor de a? Puen dase tres casos:
-Si’l valor ta ente 1 y 3 la población va estabilizase como nel casu d’antes, anque’l puntu onde para de crecer sedrá distintu.
-Si a<1 la población tarde o ceo va desaniciar. Per exemplu, con a=0,4 y Ni=0,3
-Si a>3 el sistema va entamar a facer coses perinteresantes pa los nuesos intereses. Asina pa a=3,3 y Ni=0,6:
A partir de la iteración 16, nesti exemplu, la población cimbla ente 0,8236 y 0,4794, una y otra vegada. Apaez un ciclu bianual, que si caltenemos a=3.3 va repítise pa tolos valores de Ni.
Pa otros valores de a van salinos otros resultaos. Pa a=3.5 nun tenemos dos valores, sinón cuatro que repítense ensin parar: 0,3028, 0,826, 0,5001 y 0,8750. Pa a=3.55 la población va cimblar ente ocho valores; pa a=3.56 ente 16 valores. Pero al llegar a 3,6 la repetición cíclica de valores fina, los valores baillen arriba y abaxo ensin orden, pa cualesquier población, seya lo grande que se quiera.
Nesti puntu tamos preparaos pa pintar una gráfica na que vamos representar toos estos resultaos, la exa horizontal de la gráfica representa los valores de a, y la vertical los de Ni.
Nella apaecen tolos puntos estudiaos:
-Pa a=2,5, na que la población diba fasta 0,6, correspuende-y el puntu A
-Pa a=2,7 con valor caberu 0,6296 el puntu B
-Pa a=0,4, na que la población desapaecía, puntu C
-Pa a=3,3, na que cimblaba ente dos valores, los puntos D y E
-F, G, H e I pa a=3,5, y asina con tolos valores posibles
-Pa los casos nos qu’al iterar nun atopamos valores finales, na gráfica apaecen como una llinia prieta completa, ya que tolos valores son posibles.
De tou esto, y mirando la gráfica vemos que pa tolos valores de a menores de 1 la población nun tien esficies de sobrevivir, desapaez.
Ente 1 y 3 namás qu´hai un resultáu pa cada valor, nel que la población ta n’equilibriu, ye la llinia que va desde K a L.
De magar que llegamos a L entamen les forcaes. Asina ente 3 y 3,45 namás podemos atopar dos valores, ye la nomada rexón de periodu 2, que ta ente LR y LS. En 3,45 apaecen otres dos forcaes, tamos na rexón de periodu 4. Depués atopamos la rexón de periodu 8. Tamos peraveraos a la rexón caótica, ye dicir la rexón qu’apaez depués de a=3,6, onde la población nun sigui nengún ciclu, sinón que los valores garren cualesquier valor, con una salvedá: les rexones blanques de la gráfica. Con a=3,48 apaez una rexón na que los valores de la población cimblen ente 0,1494, 0,4879 y 0,9594. Depués d’esta forcada apaez otra cuando llegamos a 3,486, que da seis valores finales ente los que cimbla la población, siguiendo les forcaes hasta otra rexón caótica.
Esto ya nos entama a sonar, ¿nun sedrá que los valores de la población tien un comportamientu fractal? Asina ye, si facemos ampliaciones a la gráfica vamos atopar que los patrones de la imaxen primera repítense hasta aburrir.
Ye nidio que la dinámica de poblaciones nun ye tan cenciella como nós la presentamos, pero modelos más refinaos tienen resultaos asemeyaos, anque nun dexen de ser modelos, la realidá ye más fragosa. Una torga perimportante ye que ye gafu algamar series temporales bastante llargues que dexen ver procesos estacionarios asemeyaos a los ya vistos o cualesquiera que seya la dinámica d’esi ecosistema.
Otra torga ye qu’al enguedeyar les coses nos modelos ya introducir una componente espacial, per exemplu, les “ventanes” periódiques lleguen cuasi a desapaecer, el caos garra les riendes, anque’l sistema siempre va tirar pal estáu descritu.
Según seyan les condiciones nel aniciu’l sistema pue seguir los pasos que ya describimos, tamién pue soceder qu’el caos faiga qu’esborre les ventanes dexando namás qu’unes intermitencies espaciu-temporales. N’otros casos el caos faise´’l dueñu, anque d’una forma estable, que caltiénse fasta’l momentu nel que'l sistema cai nel estáu d’equilibriu. Esto nun socede siempre, hai veces qu’el tiempu qu’hai qu´esperar fasta llegar al equilibriu ye encomanáu, quedando virtualmente nun estáu de caos estacionariu. Ésto tien unes implicaciones pergrandes: pue pasar que l’estáu d’un ecosistema correspuenda a una transición, ya que, realmente, nunca díbamos a llegar al estáu final, y l’estáu “normal” seya esa transición.
Esto paez separtanos del tema que nos ocupa, pero otres llinies d’investigación dan lluz a la interpretación fractal del comportamientu de los ecosistemes, como per exemplu les redes acoplaes que formen diagrames d’ondes, que pudiera ser que siguieren patrones fractales.
Modelos fechos en base a datos reales, per exemplu sobre les rellaciones ente una especie de llebre y una de llobu cerval. N’él tomaron en cuenta milenta variables vencellaes cola bioloxía de les dos especies, comportamientu, situación nel espaciu... El modelu, perabegosu y completu, esplicó perbien la dinámica de les dos especies, y coincidía colos aportáu nes estudios de diagrames de forcaes asemeyaos a los vistos.
Volvemos al modelu del aniciu, el cenciellu, onde llegaba un puntu onde, baxo determinaes condiciones, la población desapaecía. Vamos pensar qu’aquella población taba formada por tolos indivíduos d’esa especie, entós la especie desanicia.
Lo mesmo que socede en tolos ámbitos de los sistemes ecolóxicos, nel desaniciu interaicionen dellos factores: les rellaciones intra e interespecífiques, el mediu... Tou ta coneutáu. Cuando les conexones d’una especie baxen muncho desanicia, otra ocupa’l so llugar, otres queden afeutaes y puen desaniciar tamién. Si les coses pónense gafes, puede dase’l casu que'l sistema, l’ecosistema, entre nuna fas de crisis, un desaniciu lleva a otru, produzse un gran desaniciu. El procesu entama otra vegada de les cenices, hasta llegar otra vegada al estáu críticu. Les conclusiones son nidies, ye posible que’l procesu d’evolución ya’l desaniciu seya’l resultáu un procesu autoorganizáu, que quiciabes siga dellos patrones fractales. Los modelos, dixímoslo ya, son eso, modelos, imitaciones cencielles de la realidá, tovía queda muncho pa poder dicir fasta onde lleguen estes conxetures. Queden munches entrugues que retrucar sobre hasta qué puntu ye predecible la dinámica d’un ecosistema.
Existen propiedaes comunes ente la dinámica d’un ecosistema y otros sistemes dinámicos. Tal ye’l casu de la economía.
Los modelos clásicos falen d’equilibriu, en realidá son sistemes percomplexos, y qu’aseméyanse abondo a los modelos de desaniciu. Estos modelos amás de ser cenciellos, sofítanse’n supuestos ensin fundamentu empíricu y, en xeneral, nun son quien a predicir grandes movimientos bursátiles. Desque Mandelbrot trató esti tema, munchos afondaron n’él, desendolcando ferramientes d’análisis fractal que tán dando resultaos más realistes y axustaos a los datos empíricos.
Una de les principales conclusiones qu’atoparon nel aniciu foi que les series de valores económicos yeren estadísticamente autosimilares, o sía, les gráfiques yeren asemeyaes a distintes escales. Por supuestu, la dimensión, que yera fraccionaria, caltenía los sos valores alredor d’un rangu.
Nuna primer aproximación trataron de venceyar el problema col movimientu brownianu, imaxinando que los valores bursátiles yeren como una partícula que se mueve aleatoriamente p’alantre y p’atrás, siendo la representación d’esti movimientu a traviés del tiempu una gráfica.
Estudios posteriores descubrieron, por métodos d’análisis estadísticu, que la bolsa si tenía un comportamientu autosimilar, pero nun yera de tipu brownianu.
Los movimientos de los precios tán carauterizaos por discontinuidaes pergrandes que nun puen esplicase a traviés d’un movimientu continuu como ye’l movimientu brownianu, ye más les gráfiques de la evolución de los precios habría de representales en forma de gráfica de barres y non como una llinia continua.
De sobra sabemos, inda siendo profanos na materia, que la bolsa da blincos, que nin los espertos puen coñocer de mano.
Cuando’l modelu brownianu cayó munchos trataron d’inventar métodos y modelos qu'’esplicaren la dinámica d’esti sistema. En xeneral, son cosíos que faen casar los datos, como per exemplu’l métodu de “refugue de los llaos estadísticos non representativos”.
Otra vegada Mandelbrot trixo la solución, con un cambiu de paradigma. Hasta esi momentu la varianza de les series de mercáu tomábase como finita, pero Mandelbrot propuso una varianza infinita. Vamos por partes.
N’estadística s’usen dellos valores que resumen los datos, tales como la media y la desviación típica, que supuestamente marquen pa ónde tiende la población, esto val cuando esa población tien una distribución concreta (en forma de campana), pero cuando non tien esa forma la cosa cambia, los valores qu’obtenemos nun son un resumen del total. Si la población tien esa forma concreta a partir de cierto númberu de datos, los valores malapenes camuden anque aumentemos la muestra, nes series económiques los valores son cambiantes independientemente de la muestra.
La varianza ye una midida del rangu nel que se mueven los datos y nun tien dimensión, como tien la desviación típica. Mandelbrot consideró la varianza como infinita (o con valores pergrandes) por ser compatible con que la variable estudiada seya finita, y por qu’al nun tener dimensión yera aplicable a toles escales, xusto lo que necesitaba.
Axuntó’l principiu d’autosimilaridá cola idea de que los cambeos de precios son independientes, qu’amás tienen una variabilidá pergrande, pa desendolcar modelos sofitaos en datos económicos reales. Él y otros atoparon que los precios caltienen los sos patrones a distintes escales.
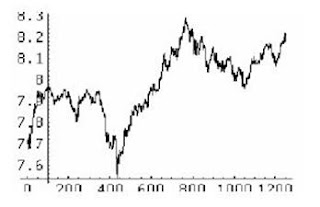
Exemplu paradigmáticu ye’l que resultó d’estudiar los precios del algodón n’USA. Vemos la gráfica abaxo.
El fechu que la economía siga patrones nun quier dicir qu’algún día podamos predicir pa ónde va dir ésta, como socede en tolos procesos dinámicos complexos intervienen munchos factores pa poder facer predicciones a llargo plazu.










Comentarios
Publicar un comentario